A few months ago, I published a discussion on the use of a simple linear auto-regression to segment references to monetary figures in natural language. The short post I am making today will document some results from a small experiment I ran on improving this model’s generalization using text-augmentation.

Model Review

Recall that our model computes a confidence for each character in a string \(s\) where the inference \(\sigma(s, i)\) at character \(i\) takes as input the result of the inference \(\sigma(s, i - 1)\) at the proceeding character along with a vector representation \(v(i)\) of the characters around character \(i\). Given these terms, our character level inference without the autoregressive component and zero-to-one normalization takes the value:

\[\sum_{j=1}^{|v(i)|} \phi_j v(i)_j + b\]

Given a constant auto-regressive prior, a larger value from the computed expression above indicates that character \(i\) ins \(s\) is more likely to be a part of a positive segment.

In our earlier work, \(v(i)\) was taken simply to be the concatenation of the 1-hot encoding of characters in a window about \(i\). While this representation is simple to work with, it has the disadvantage of being a sparse-encoding of our vector window. In particular, given a window size \(W\) and a character set of size \(N_\mathcal{A}\), the vector \(v(i)\) has dimension \(WN_\mathcal{A}\).

For our particular application, the sparse vector representation of \(v(i)\) amounted to learning \(O(1000)\) parameters from only \(O(100)\) data points. If we model our problem by assuming that positive segments and negative segments are drawn from distinct probability distributions, it is likely that there is insufficient data to accurately model these two distributions. Though the negative distribution is likely too complex to describe by an explicitly model (it is hard to model the English language), the positive distribution (references to monetary values) is relatively simple and can probably be convincingly modeled by writing an explicit generating function, which we can then use to augment our training data.

Experimentation

We start with a labeled dataset \(\mathcal{D}\) consisting of the monetary-reference text-segmentation dataset we detailed here. At the time of writing, this dataset consisted of 80 short segmented strings which we partitioned into training \(\mathcal{D}_{tr}\) and test \(\mathcal{D}_{te}\) sets. Based on our discussion above, we propose an experiment as follows:

1. Write a generating function \(g\) which can produce strings from a distribution similar to that of positive text.
2. For a labeled string we can replace each discrete positive segment with a string generated by \(g\), updating the example’s label to account for the new length of the generated segment. We perform this a large number \(\hat{n}\) of times for each string in \(\mathcal{D}_{tr}\), giving us a larger training dataset \(\hat{\mathcal{D}}_{tr}\) of size \(\hat{n} \vert\mathcal{D}_{tr}\vert\).
3. Train a model \(T\) on \(\mathcal{D}_{tr}\) and an augmented model \(\hat T\) on \(\hat{\mathcal{D}}_{tr}\). Compare the performance of these two models on the same unaugmented test dataset \(\mathcal{D}_{te}\).

For the experiment we present, we took we chose our test and train sets to estimate the performance of \(T\) and \(\hat T\) using leave-one-out cross validation, taking \(\hat n = 10\) for each 1-fold. We evaluate each trained model in the same way we do in our original post on text segmentation.

The Generating Function

It is important to document possible generators as the performance of the augmented model likely depends considerably on our choice of generating function. For our application, generating references to monetary amounts, one might naively try to generate numbers that fall within some reasonable range. However, we felt that such an approach discards a lot of important subtlety from the distribution. For instance, such an approach completely eliminates punctuation present in the true distribution and furthermore fails to consider the tendency for monetary references to generally take “nicely rounded” values such as 25.

Instead of manually designing our generating function to explicitly consider all these statistical tendencies, we instead proceed by modifying a bootstrapped sample taken from our original data. That is, to approximately sample a new point from the true positive distribution, we start by uniformly randomly choosing \(s\) from our small true sample of positive segments. Then, for each numerical character in \(s\) that is not 0 or 5, we replace that character with a random numeric character chosen from 1-9 at random.

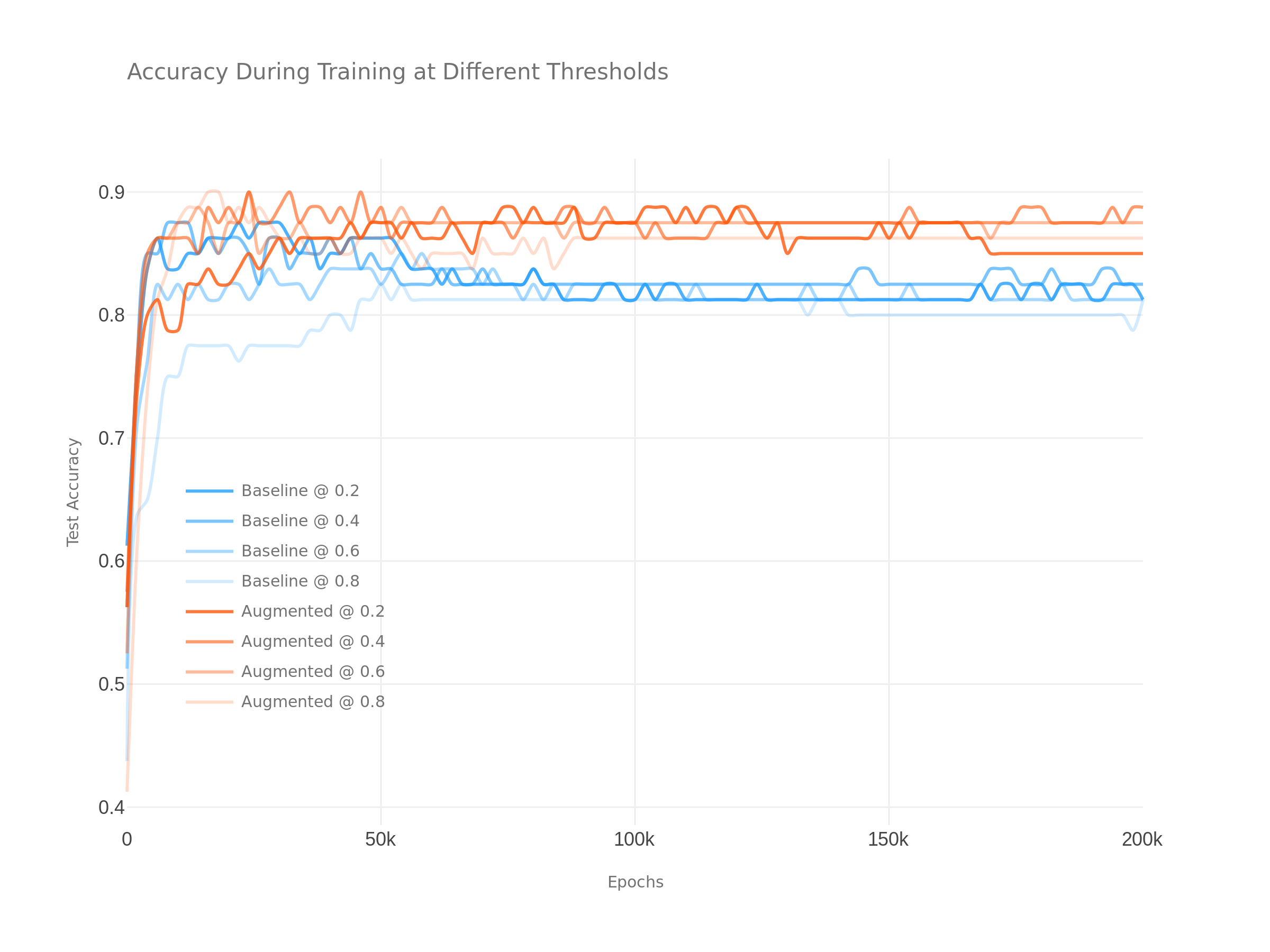
Results

The following plots show the performance of \(T\) in blue versus \(\hat T\) in red at a range of label thresholds. As you can see from this, the augmented model exhibits both slightly improved performance as well as increased resistance to over-fitting as we increase our training epochs.